حاسبة التيار والجهد لسلسلة دوائر RLC
حاسبة التيار والجهد لسلسلة دوائر RLC رنين
آلة حاسبة لحساب الممانعة والتيار المار والجهد عبر المقاوم والمكثف والمحث في سلسلة. تعطي الآلة الحاسبة المعاوقة المكافئة لجميع المكونات الثلاثة المتسلسلة ، التيار والجهد كأرقام مركبة في الأشكال القطبية. مرجع المرحلة هو أن طور جهد المصدر ويفترض أنه صفر
\( \) \( \) \( \)معادلة للمقاومة والتيار والجهد في سلسلة دوائر RLC المستخدمة في الآلة الحاسبة ووحداتها
نعطي أولاً المعادلات المستخدمة في سلسلة حاسبة RLC.دائرة الرنين
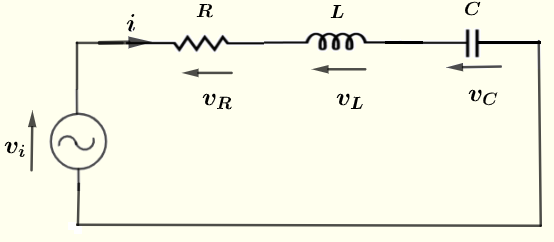
دع \( f \) أن يكون التردد بالهرتز لجهد المصدر \( v_i \) توفير الدائرة وتحديد المعلمات التالية المستخدمة في الحسابات
\( \omega = 2 \pi f \) , التردد الزاوي في راديان / ثانية
\( X_C = 1 / (\omega C) \) in \(\Omega \) , مفاعلة المكثف مع السعة \( C \).
\( X_L = \omega L \) in \(\Omega \) , مفاعلة الحث مع الحث \( L \).
دع \( Z \) تكون المعاوقة المكافئة لدائرة RLC المتسلسلة الموضحة أعلاه وكتابتها في شكل قياسي معقد على النحو التالي \[ Z = R +j (X_L - X_C) \] وفي شكل قطبي معقد كما يلي \[ Z = |Z| \; \angle \; \theta \] حيث المعامل \( |Z| \) وبفتراض \( \theta \) of \( Z \) أعطيت من قبل
معامل: \( |Z| = \sqrt {R^2 + (X_L - X_C)^2 } \) في اوم \( (\Omega) \)
دعوى: \( \theta = \arctan \left(\dfrac{X_L - X_C}{R} \right) \) بالراديان أو الدرجات
دع \( v_i = V_0 \cos(\omega t) \)
دع \( I \), \( V_C \), \( V_L \) and \( V_R \) تكون الأشكال المعقدة في شكل قطبي للتيار \( i \), \( v_C \), \( v_L \) و \( v_R \) في الدائرة.
\( I = \dfrac{V_0}{Z} = \dfrac{V_0}{|Z|} \; \angle \; -\theta \)
\( V_C = I (- j X_C) = \dfrac{V_0}{|Z|} X_C \; \angle \; -\theta - 90\)
\( V_L = I (X_L j) = \dfrac{V_0 \cdot X_L}{|Z|} \; \angle \; -\theta + 90\)
\( V_R = I R = \dfrac{V_0 R}{|Z|} \; \angle \; -\theta \)
ملاحظة
1) أن يتم قياس جميع المراحل مع الأخذ في الطور \( v_i \) كمرجع.
2) يوجد حل رقمي في أسفل هذه الصفحة للقيم الافتراضية لقيمة ذروة جهد المنبع ، والمقاومة ، والسعة ، والحث والتردد في هذه الآلة الحاسبة.
استخدام الآلة الحاسبة
أدخل قيمة ذروة جهد المصدر \( V_0\), المقاومة \( R \), المتسعة \( C \), المحث \( L \) التردد \( f \) كأرقام حقيقية موجبة بوحدات معينة ثم اضغط على "حساب".الناتج هنا
مثال نظري او عددي باستخدام الصيغ مذكورة اعلاة
دع \( V_i = 10 ; \angle \; 0 \)
التردد \( f = 1 \; kHz \) , \( C = 10 \; \mu F \) , \( L = 10 \; mH \) and \( R = 100 \; \Omega \)
\( X_L = \omega L = 2 \pi f L = 2 \pi 10^3 10^{-2} = 62.83 \; \Omega \)
\( X_C = \dfrac{1}{\omega C} = \dfrac{1}{2 \pi f C} = \dfrac{1}{2 \pi 10^3 10^{-5} } = 15.92 \; \Omega \)
مجموعة المصطلحات التخيلية
\( Z = 100 + j ( 62.83 - 15.92 ) \)
تبسيط
\( Z = 100 + j ( 62.83 - 15.92 ) = 100 + 46.91 j\)
في شكل طور
\( Z = 110.45 \; \angle \; 25.13^{\circ} \)
\( I = \dfrac{V_0}{Z} = \dfrac{V_0}{|Z|} \; \angle \; -\theta \)
\( \quad \quad = \dfrac{10}{110.45} \; \angle \; - 25.13 ^{\circ} = 0.091 \; \angle \; - 25.13 ^{\circ} \)
\( V_C = I (- j X_C) = \dfrac{V_0 \cdot X_C}{|Z|} \; \angle \; -\theta - 90\)
\( \quad \quad = \dfrac{10 \cdot 15.92 }{110.45} \; \angle \; - 25.13 - 90 = 1.441 \; \angle \; -115.13 ^{\circ} \)
\( V_L = I (X_L j) = \dfrac{V_0 \cdot X_L}{|Z|} \; \angle \; -\theta + 90\)
\( \quad \quad = \dfrac{10 \cdot 62.83 }{110.45} \; \angle \; - 25.13 + 90 = 5.689 \; \angle \; 64.87 ^{\circ} \)
\( V_R = I R = \dfrac{V_0 R}{|Z|} \; \angle \; -\theta \)
\( \quad \quad = \dfrac{10 \cdot 100 }{110.45} \; \angle \; - 25.13 = 9.054 \; \angle \; - 25.13^{\circ} \)